|
Errata for
Elementary Real Analysis
(2008 Edition)
(Courtesy Professor H. P. Boas)
|
This page of errata was prepared by Professor Harold P. Boas who taught a course using this text at Texas A&M University.
For his original web page please visit:
What follows is simply a copy of his comments.
Comments on the textbook
- Exercise 1.3.3
- The discussion is incomplete. One needs to check additionally that
the supposed subfield contains the additive and multiplicative
identity elements and contains for each of its nonzero elements the
additive and multiplicative inverses. The same comment applies to
Note 1 at the end of the chapter.
- Section 1.10
- In the paragraph titled “Properties of the Distance
Function”, item 3, there is a duplicated closing
right-hand parenthesis at the end of the sentence.
- Note 7 for Chapter 1
- For (x
   2 2 y y 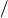 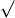 2) read (x 2) read (x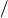 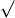 2 2 y y 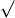 2) 2)
- Exercise 2.9.1
- In part (a), the right-hand side should be sn+1−
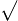 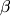 
- Section 2.11
- In the paragraph preceding Theorem 2.40, one of the date
ranges is set with a hyphen and the other with an en dash. The
latter punctuation is standard.
- Section 2.12
- In Example 2.42, sixth sentence, for “the N stage” read
either “stage N” or “the Nth stage”.
- Chapter 2, Note 26
- For 1
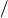 6 read 1 6 read 1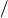 16 16
- Chapter 2, Note 29
- In the second displayed formula, the expression y−n+2m
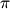 is
intended to be y−(n+2m is
intended to be y−(n+2m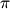 ) (although the sign change does not
much matter, since m is arbitrary). ) (although the sign change does not
much matter, since m is arbitrary).
- Section 4.1
- In the second sentence, Heine's personal name should be spelled
“Eduard” according to the discussion just above
Definition 4.28 later in the chapter.
- Section 4.2.3
- In Example 4.6, item 1, there is a spurious doubled
right-hand parenthesis at the end of the sentence.
- Section 4.3.1
- In Example 4.10, item 2, insert the word “is”
preceding “not closed”.
- Exercise 4.3.23
- In part (b), add a question mark at the end of the first sentence.
- Section 4.5, proof of Theorem 4.33
- In the second paragraph, second
sentence, the (correct) statement “there exists
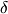 (x) (x)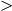 0 for
which (x−t 0 for
which (x−t x+t) x+t) Ux for all t Ux for all t (0 (0 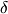 (x))” is a convoluted way of saying “there
exists a positive number (x))” is a convoluted way of saying “there
exists a positive number 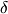 (x) such that the interval (x− (x) such that the interval (x−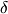 (x) (x) x+ x+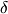 (x)) is a subset of Ux”. The
intended statement is probably the equivalent statement “there exists (x)) is a subset of Ux”. The
intended statement is probably the equivalent statement “there exists 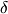 (x) (x) 0 for
which [x−t 0 for
which [x−t x+t] x+t] Ux for all t Ux for all t (0 (0 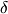 (x))” (for the construction of a Cousin cover
requires the consideration of closed intervals). A similar
comment applies to the sixth sentence in the paragraph. (x))” (for the construction of a Cousin cover
requires the consideration of closed intervals). A similar
comment applies to the sixth sentence in the paragraph.
- Exercise 4.5.18
- The name of the Finnish mathematician
Lindelöf is misspelled with a doubled terminal consonant. The
same error appears in Exercise 4.5.19 and in Note 83 at
the end of the chapter.
- Exercise 4.7.4
- The four statements do not parse. Part (a) should begin,
“Let A=[0
 1] 1] Describe […]”, and similarly for the
other parts. Describe […]”, and similarly for the
other parts.
- Exercise 4.7.10
- This exercise is identical to Exercise 4.5.10.
- Exercise 4.7.15
- In part (d), the word “interval” has to be
interpreted to allow, as a special case, a single point (a
degenerate interval).
- Section 5.2.3
- In Exercise 5.2.12, insert a period between
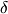 2 and
“Define”. And after Exercise 5.2.16, delete the
orphaned period. 2 and
“Define”. And after Exercise 5.2.16, delete the
orphaned period.
- Section 5.2.4
- In the first line of the proof of Corollary 5.24, for
“first of the these” read “first of these”.
- Section 5.2.5
- At the end of the first paragraph, the claimed falsity arises only
because one or both sides of the equation can be undefined. See also Exercise 5.2.23.
- Section 5.2.6
- Most authors use the terminology “Dirichlet function”
to refer to the characteristic function of the rational numbers,
since Dirichlet considered the example of a function that takes a
constant value c on the rationals and a different constant
value d on the irrationals [Sur la convergence des
séries trigonométriques qui servent à
représenter une fonction arbitraire entre des limites
données, Journal für die reine und angewandte
Mathematik 4 (1829) 157–169; see p. 169]. The
function called “Dirichlet function” in the text
seems to be due to Karl Johannes Thomae [Einleitung in die Theorie der
bestimmten Integrale, 1875, p. 14] and is commonly known
as “the ruler function”.
- Exercises 5.4.7 and 5.4.8
- The punctuation mark at the end should be a period, not a comma.
- Section 5.9.3
- In the proof of Theorem 5.64, third paragraph, the pointsa and b such that a
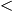 b b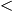 c are not the points a
and b in the statement of the theorem. c are not the points a
and b in the statement of the theorem.
- Chapter 5, Notes
- In Note 107, there is no need to assume positivity, for the exercise has
absolute values in it.
- In Note 109, for “sum and products rule” read
“sum and product rules”.
- Note 118 does not respond to the statement of the exercise, for
there is no “same collection” at hand, and applying
Cousin's lemma is not in the spirit of the instruction to
“[a]djust the proof of Theorem 5.48”. Actually,
the given proof of Theorem 5.48 carries over almost word for
word.
- In Note 137, the claim that “[t]he function must be
onto” is false. For instance, the function might be a
constant function. The statement of the exercise is nonetheless
true. You can apply the intermediate-value property to the
function that sends x to f(x)−x

- Section 7.2.1
- The parenthetical remark preceding Example 7.4 needs a
terminal period.
- Section 7.3.1
- Equation (4) in the proof of Theorem 7.7 has an error:
the term −f(x) should be −f(x0)

- In Exercise 7.3.2, for “Figure fig-table2” read
“Figure 7.3”.
- Section 7.3.3
- In the second paragraph, second sentence, for “that
that” read “that”.
- The argument in the third paragraph does not prove what is
claimed. The calculation determines the derivative of the inverse
function under the hypothesis that the inverse function is
differentiable. But what is claimed is that the inverse
function is, in fact, differentiable. That fact is proved later in
Theorem 7.32 of Section 7.9.
- Exercise 7.4.2
- In part (a), both instances of f without a subscript
should be fn

- Exercise 7.6.2
- The statement of the exercise is incorrect, for the equation
x3+3x2−4
has both −2 and 1 as solutions. The statement of the exercise
can be corrected by replacing “cannot have more than one
solution” with “cannot have more than one positive
solution”. Alternatively, add the hypothesis that 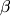 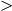 0. 0.
- Exercise 7.6.8
- The unidentified letter M denotes a fixed positive real number (a constant).
- Exercise 7.6.18
- The statement of the exercise is incorrect. If f(x)=x2, then f has a continuous second derivative, yet the indicated limit is equal to 2
 not 0 not 0 The intended statement is that the limit exists, not that the limit equals 0 The intended statement is that the limit exists, not that the limit equals 0
- Section 7.7
- In the Note following Definition 7.22, third sentence, delete the unmatched closing right-hand parenthesis.
- Section 7.8
- Example 7.29 is incorrectly stated. The function g is supposed
to be the characteristic function of the rational numbers, not the irrationals.
- In the proof of Theorem 7.30, first displayed formula, delete
the spurious closing right-hand parenthesis preceding the closing
right-hand bracket.
- In the proof of Theorem 7.30, third paragraph, insert a
space after the period that ends the first sentence.
- Section 7.9
- In the second paragraph, third sentence, “the extreme
value” is misleading, for there is not a unique extremum. The
point is that if f
 (a) (a)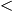 0 0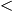 f f (b), then the global minimum
cannot occur at an endpoint and hence occurs at an interior point;
if f (b), then the global minimum
cannot occur at an endpoint and hence occurs at an interior point;
if f (b) (b)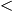 0 0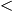 f f (a), then the global maximum cannot occur at
an endpoint and hence occurs at an interior point. (a), then the global maximum cannot occur at
an endpoint and hence occurs at an interior point.
- Section 7.10
- In the line preceding equation (14), insert a period before “Then”.
- In Exercise 7.10.13, some hypothesis on the set A is needed
to guarantee convergence of the series; boundedness ofA will do.
- Section 7.11
- In the paper version, the section titles and the page headers are
missing the letter ô in the name L'Hôpital. The pdf
version for screen viewing is correct.
- Example 7.37, second paragraph, two-line display, the derivativeg
 (x) should be 3+15x2, not 3+5x2 (x) should be 3+15x2, not 3+5x2
- Proof of Theorem 7.38, third paragraph, third sentence,
“contradicting hypothesis (ii)” should say
“contradicting hypothesis (iii)”.
- Proof of Theorem 7.41, last line, add a period.
- In Exercise 7.11.1(c), the terminal punctuation should be a
question mark.
- Exercise 7.13.1
- The given condition contains no information about the value of the function f at the point x0
 so the property cannot possibly be equivalent to differentiability of f at x0 so the property cannot possibly be equivalent to differentiability of f at x0 The property is, however, equivalent to the statement that f has a removable singularity at x0 The property is, however, equivalent to the statement that f has a removable singularity at x0 and the function obtained by removing the singularity is differentiable at x0 and the function obtained by removing the singularity is differentiable at x0 An analogous issue arises in Exercise 7.13.2. An analogous issue arises in Exercise 7.13.2.
- Exercise 7.13.11
- The name “Chisholm” is missing the
letter “h”.
- Chapter 7, Notes
- In Note 187 for Exercise 7.6.8, the name Lipschitz is misspelled (the letter c is missing).
- In Note 201 for Exercise 7.8.9, the words “For an
example” should go with the first sentence, not the second
sentence. (The first sentence of the hint pertains to the second part
of the exercise, while the second sentence of the hint pertains to
the first part of the exercise.)
- In Note 202 for Exercise 7.8.10, some hypothesis is needed on the
set A to guarantee convergence of the series; boundedness ofA will do.
- In Note 203 for Exercise 7.9.1, the condition f(0)=0 is
supposed to be f
 (0)=0 (0)=0
- In Note 211 for Exercise 7.10.14, the punctuation at the end of
the second line of the
three-line display is awry.
- In Note 215 for Exercise 7.11.10, the hint should say that
The denominator g
 (x) is missing. (x) is missing.
- Section 8.2
- The first sentence of Corollary 8.3 is missing its terminal period.
- Exercise 8.3.1
- In the first displayed formula, delete the spurious vertical bar
following [a
 b] b]
- Section 8.6
- In Example 8.14, end of first paragraph, for “and
to” read “and”.
- In the proof of Theorem 8.17, fourth displayed equation,
the closing right-hand parenthesis is missing after
the argument of
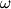 f. f.
- Exercise 8.10.1
- In the first displayed formula, infm(f
 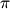 ) should be supm(f ) should be supm(f 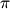 ) )
- Chapter 8, Notes
- In Note 239 for Exercise 8.9.2, delete the spurious letter
“x” at the end of the line.
- Appendix A
- In Section A.2, the paragraph about Set-Builder Notation, delete the spurious
closing right-hand parenthesis at the end of the second sentence.
- In Section A.5, third paragraph, the Latin wordreductio is a noun, not a verb, so the translation is
“reduction”, not “I reduce”. In the
subsequent indented paragraph, there is a spurious space between
the symbol Q and the period; in the pdf version, the period
consequently has gotten displaced to a separate line.
- At the end of Exercise A.8.8, the phrase “well ordering
of
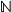 ” is mysteriously repeated. ” is mysteriously repeated.
- In Section A.9, end of second paragraph, the phrase
“there do exist numbers” should be in the
indicated example “there does exist a number”.
- In Note 388, the closing delimiter after the date range should
be a parenthesis, not a square bracket.
Harold P. Boas  | | |
| | |
|
|