|
#5. It clears up the mystery of the popcorn function.
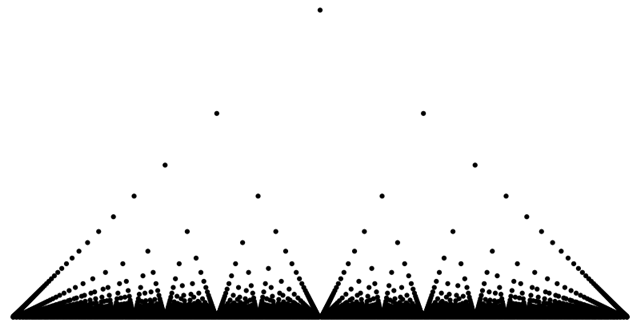
Suppose
a function is zero at every irrational point. What is its integral?
Well, certainly, the points left out are insignificant. Not merely a set
of measure zero but even countable. Such a set plays no role in
determining the integral so your function can have any values on the
rationals, or even remain undefined on the rationals. The simple answer
is that your function is integrable on every interval with a zero
integral.
Oh, what? Sorry? You have only learned the Riemann
integral. Alas, the answer now is entirely different. Now the function
must be defined at these missing rational points and the answer depends
on how you define them. If the resulting function is integrable then
certainly the value of the integral is zero, but it may or may not be
integrable. Let xn be a listing of all the rationals and let your function be defined to be f(xn)=cn and with f(x)=0 at x irrational. What is a necessary and sufficient condition for f
to be integrable [i.e., integrable in the dumb Riemann sense]? That's a
tough question, but one that is not particularly important.
In
1875, K. J. Thomae discovered the now-famous example of a function of
this kind that is continuous at all the irrationals and discontinuous at
the rationals. This function has many names: the modified Dirichlet
function, Thomae function, Riemann function, raindrop function, ruler
function, and popcorn function.
His
example is a nice curiosity in the study of continuous functions. But
it is usually presented to students of integration theory as example of a
seriously discontinuous function that is integrable. The student gets
the impression that it is important to have continuity, that
discontinuities must be controlled, that without proper configuration of
the values of a function the integral is badly affected, and that
integration theory has its mysteries. That's good teaching?
If we
drop the Riemann integral then the popcorn function would not be
mentioned in the context of integration theory and can return to its
proper place in the study of continuity.
Is there a function continuous at every rational and discontinuous at every irrational?
Is there a function discontinuous at every rational and continuous at every irrational?
The answer to the first question is "no" and the answer to the second question is "popcorn."
Top ten reasons for dumping the Riemann integral: #10, #9, #8, #7, #6, #5, #4, #3, #2, #1
|
 |
 |
Olypian quarrels et gorilla congolium sic ad nauseum.
|
 |
Olypian quarrels et gorilla congolium sic ad nauseum.
|
 |
Olypian quarrels et gorilla congolium sic ad nauseum.
| |
 |
 |
 |
Olypian quarrels et gorilla congolium sic ad nauseum.
|
 |
Olypian quarrels et gorilla congolium sic ad nauseum.
|
 |
Olypian quarrels et gorilla congolium sic ad nauseum.
| |
 |
 |
 |
Olypian quarrels et gorilla congolium sic ad nauseum.
|
 |
Olypian quarrels et gorilla congolium sic ad nauseum.
|
 |
Olypian quarrels et gorilla congolium sic ad nauseum.
| |